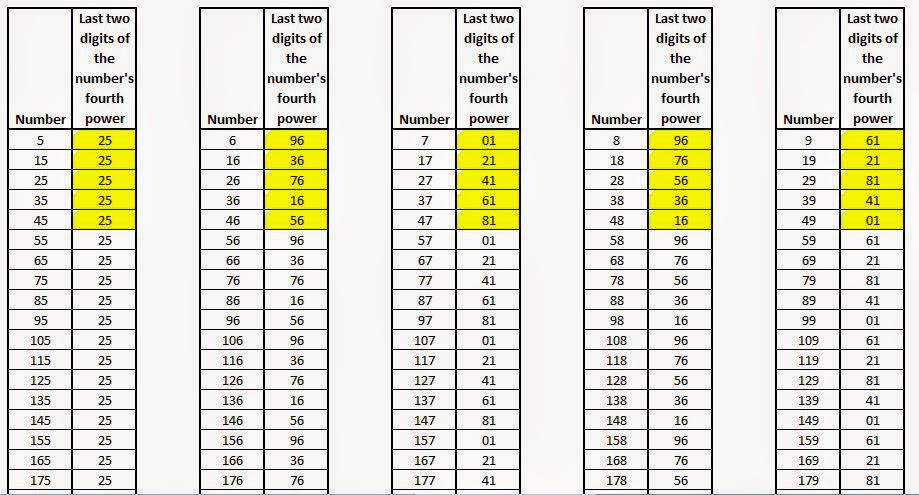
The procedure:
Take any number (Say x).
Form a set of numbers by adding 10 (Your set={x,x+10,x+20,x+30,...}).
Raise every member of the obtained set to its fourth power.
Observe the last two digits (taken from right to left) of the obtained fourth powers.
The last two digits of the fourth powers repeat after every five members of the set.
The Proof:
Any 6 terms of the series will be of the format x,x+10,x+20,x+30,x+40,x+50.
We need to prove that the pattern of the fourth powers repeats after every 5 terms.
Therefore, it suffices to prove that the digits at the unit place and tens place of fourth power of a number are equal when the number after five terms is raised to the fourth power.
Therefore, we need to prove that the last two digits of the fourth power of x and the fourth power of x+50 are equal. (Since the numbers are taken at a difference of 10 and there are 5 such terms.)
Similarly, last two digits of fourth powers of x+10 and x+60 will be equal.
Similarly, last two digits of fourth powers of x+20 and x+70 will be equal.
And so on ...
Thus, the pattern continues to repeat after every five terms.
Example:
We choose 4 as our number.
The set of numbers obtained is {4,14,24,34,44,54,64,74,84,94,104,114,...}.
We raise the terms of this set to their fourth powers {256,38416,331776,1336336,3748096,8503056,16777216,29986576,49787136,78074896,116985856,168896016...}.
We observe the last two digits of the obtained fourth powers {56,16,76,36,96,56,16,76,36,96,56,16...}.
The pattern {56,16,76,36,96} repeats itself.
Derived Corollary:
The last two digits of a number's fourth power and another number's fourth power are the same when another number is formed by adding a multiple of 50 to the first number.
Example of the corollary:
We choose 6 as our first number.
We add multiples of 50 to 6. {6,56,156}
We raise these numbers to their fourth powers. {1296,9834496,592240896}
The last two digits of the numbers obtained are the same, i.e. 9 and 6.
Important Observation:
If any number has 5 at its unit place, its fourth power ends with 2 and 5 at ten's and unit's place respectively. (This, too can be proved easily)
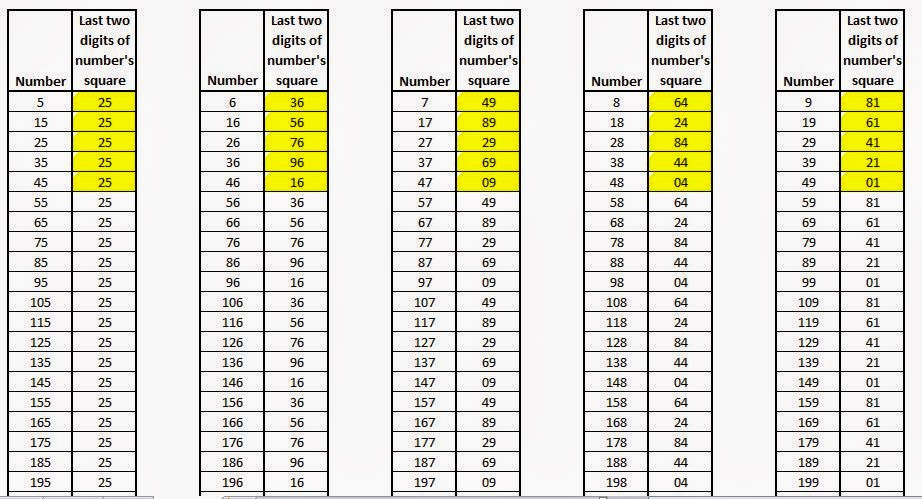
A similar pattern is observed in the cubes of even numbers and in the squares of numbers .
Q.E.D
© Rishabh Bidya
Take any number (Say x).
Form a set of numbers by adding 10 (Your set={x,x+10,x+20,x+30,...}).
Raise every member of the obtained set to its fourth power.
Observe the last two digits (taken from right to left) of the obtained fourth powers.
The last two digits of the fourth powers repeat after every five members of the set.
The Proof:
Any 6 terms of the series will be of the format x,x+10,x+20,x+30,x+40,x+50.
We need to prove that the pattern of the fourth powers repeats after every 5 terms.
Therefore, it suffices to prove that the digits at the unit place and tens place of fourth power of a number are equal when the number after five terms is raised to the fourth power.
Therefore, we need to prove that the last two digits of the fourth power of x and the fourth power of x+50 are equal. (Since the numbers are taken at a difference of 10 and there are 5 such terms.)
Similarly, last two digits of fourth powers of x+20 and x+70 will be equal.
And so on ...
Thus, the pattern continues to repeat after every five terms.
Example:
We choose 4 as our number.
The set of numbers obtained is {4,14,24,34,44,54,64,74,84,94,104,114,...}.
We raise the terms of this set to their fourth powers {256,38416,331776,1336336,3748096,8503056,16777216,29986576,49787136,78074896,116985856,168896016...}.
We observe the last two digits of the obtained fourth powers {56,16,76,36,96,56,16,76,36,96,56,16...}.
The pattern {56,16,76,36,96} repeats itself.
Derived Corollary:
The last two digits of a number's fourth power and another number's fourth power are the same when another number is formed by adding a multiple of 50 to the first number.
Example of the corollary:
We choose 6 as our first number.
We add multiples of 50 to 6. {6,56,156}
We raise these numbers to their fourth powers. {1296,9834496,592240896}
The last two digits of the numbers obtained are the same, i.e. 9 and 6.
Important Observation:
If any number has 5 at its unit place, its fourth power ends with 2 and 5 at ten's and unit's place respectively. (This, too can be proved easily)
A similar pattern is observed in the cubes of even numbers and in the squares of numbers .
Q.E.D
© Rishabh Bidya