Pattern in squares of numbers : Last two digits of squares of numbers at a difference of 10

The procedure:

Take any number (Say x).

Form a set of numbers by adding 10 (Your set={x,x+10,x+20,x+30,...}).

Square every member of your obtained set.

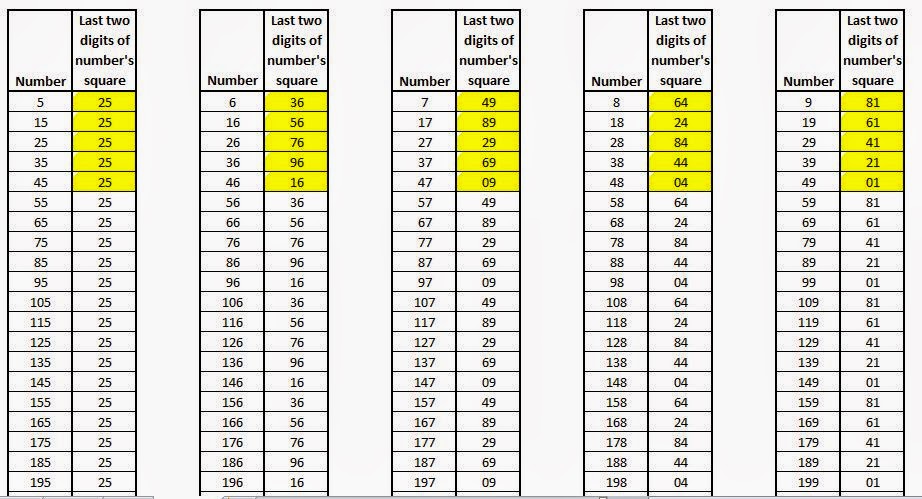
Observe the last two digits (taken from right to left) of the obtained squares.

The last two digits of the squares repeat after every five members of the set.

The Proof: 

Any 6 terms of the series will be of the format x,x+10,x+20,x+30,x+40,x+50.

We need to prove that the last two digits of the square of x and the square of x+50 are equal.

Similarly, last two digits of squares of x+10 and x+60 will be equal.

Similarly, last two digits of squares of x+20 and x+70 will be equal.

And so on ...

Thus, the pattern continues to repeat after every five terms.

Example:

We choose 4 as our number.

The set of numbers obtained is {4,14,24,34,44,54,64,74,84,94,104,114,...}.

We square the members of the obtained set {16,196,576,1156,1936,2916,4096,5476,7056,8836,10816,12996,...}.

We observe the last two digits of the obtained squares {16,96,76,56,36,16,96,76,56,36,16,96,...}.

The pattern {16,96,76,56,36} repeats itself.

Derived Corollary:

The last two digits of a number's square and another number's square are the same when another number is formed by adding a multiple of 50 to the first number. 

Example of the corollary:

We choose 6 as our first number.

We add multiples of 50 to 6. {6,56,156,306}

We square these numbers. {36,3136,24336,93636}

The last two digits of the numbers obtained are the same, i.e. 3 and 6.

Important Observation: 

If any number has 5 at its unit place, it ends with 2 and 5 at ten's and unit's place respectively. (This, too can be proved easily)

A similar pattern is observed in the cubes of even numbers. Pattern in cubes of even numbers at a difference of 10

Q.E.D

© Rishabh Bidya